3D-Kollisionsdetektion

Dieser Artikel bietet eine Einführung in die verschiedenen Begrenzungsvolumentechniken, die zur Implementierung der Kollisionsdetektion in 3D-Umgebungen genutzt werden. Folgeartikel werden Implementierungen in spezifischen 3D-Bibliotheken behandeln.

Achsen-ausgerichtete Begrenzungsboxen

Wie bei der 2D-Kollisionsdetektion sind achsen-ausgerichtete Begrenzungsboxen (AABB) der schnellste Algorithmus, um zu bestimmen, ob die beiden Spielelemente sich überschneiden oder nicht. Diese Methode besteht darin, Spielelemente in eine nicht gedrehte (daher achsen-ausgerichtete) Box einzuschließen und die Positionen dieser Boxen im 3D-Koordinatenraum zu überprüfen, um zu sehen, ob sie sich überschneiden.

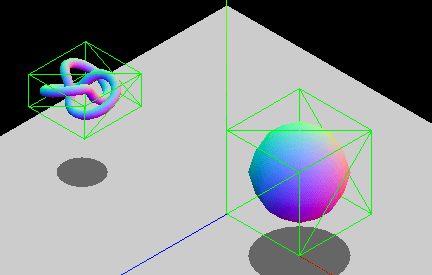
Zwei dreidimensionale, nicht quadratische Objekte, die im Raum schweben und von virtuellen rechteckigen Boxen umgeben sind.

Die achsen-ausgerichtete Einschränkung existiert aus Leistungsgründen. Der Überlappungsbereich zwischen zwei nicht gedrehten Boxen kann allein mit logischen Vergleichen überprüft werden, während gedrehte Boxen zusätzliche trigonometrische Operationen erfordern, die langsamer zu berechnen sind. Wenn Sie Elemente haben, die rotieren werden, können Sie entweder die Dimensionen der Begrenzungsbox anpassen, sodass sie das Objekt weiterhin einhüllt, oder eine andere Begrenzungsgeometrie wie Kugeln verwenden (die rotationsinvariant sind). Das untenstehende animierte GIF zeigt ein grafisches Beispiel einer AABB, die ihre Größe an das rotierende Element anpasst. Die Box ändert ständig ihre Dimensionen, um das darin enthaltene Element passgenau zu umschließen.

Animiertes rotierendes Knotenmuster, das zeigt, wie die virtuelle rechteckige Box beim Rotieren der Knoten schrumpft und wächst. Die Box dreht sich nicht.

Hinweis: Schauen Sie sich den Artikel Begrenzungsvolumen mit Three.js an, um eine praktische Implementierung dieser Technik zu sehen.

Punkt vs. AABB

Zu überprüfen, ob ein Punkt innerhalb einer AABB liegt, ist ziemlich einfach — wir müssen nur überprüfen, ob die Koordinaten des Punktes innerhalb der AABB liegen, wobei jede Achse separat betrachtet wird. Wenn wir annehmen, dass P_x, P_y und P_z die Koordinaten des Punktes sind und B_minX–B_maxX, B_minY–B_maxY, und B_minZ–B_maxZ die Bereiche jeder Achse der AABB sind, können wir mit der folgenden Formel berechnen, ob eine Kollision zwischen den beiden stattgefunden hat:

f(P, B)= (P_x \ge B_{minX} \wedge P_x \le B_{maxX}) \wedge (P_y \ge B_{minY} \wedge P_y \le B_{maxY}) \wedge (P_z \ge B_{minZ} \wedge P_z \le B_{maxZ})

Oder in JavaScript:

function isPointInsideAABB(point, box) {
  return (
    point.x >= box.minX &&
    point.x <= box.maxX &&
    point.y >= box.minY &&
    point.y <= box.maxY &&
    point.z >= box.minZ &&
    point.z <= box.maxZ
  );
}

AABB vs. AABB

Ob eine AABB eine andere AABB schneidet, lässt sich ähnlich wie beim Punkt-Test überprüfen. Wir müssen nur einen Test pro Achse durchführen, wobei wir die Begrenzungen der Boxen verwenden. Das untenstehende Diagramm zeigt den Test, den wir über die X-Achse durchführen würden — im Grunde überlappen sich die Bereiche A_minX–A_maxX und B_minX–B_maxX?

Handgezeichnetes Bild von zwei Rechtecken, das die Überlappung der oberen rechten Ecke von A mit der unteren linken Ecke von B zeigt, da A's größte x-Koordinate größer ist als B's kleinste x-Koordinate.

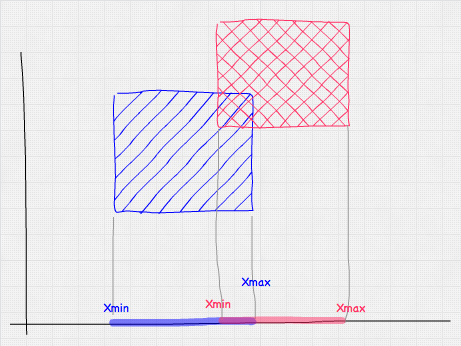
Mathematisch würde das so aussehen:

f(A, B) = (A_{minX} \le B_{maxX} \wedge A_{maxX} \ge B_{minX}) \wedge ( A_{minY} \le B_{maxY} \wedge A_{maxY} \ge B_{minY}) \wedge (A_{minZ} \le B_{maxZ} \wedge A_{maxZ} \ge B_{minZ})

Und in JavaScript würden wir dies verwenden:

function intersect(a, b) {
  return (
    a.minX <= b.maxX &&
    a.maxX >= b.minX &&
    a.minY <= b.maxY &&
    a.maxY >= b.minY &&
    a.minZ <= b.maxZ &&
    a.maxZ >= b.minZ
  );
}

Begrenzungskugeln

Das Verwenden von Begrenzungskugeln zur Kollisionsdetektion ist etwas komplexer als AABB, aber immer noch ziemlich schnell zu testen. Der Hauptvorteil von Kugeln ist, dass sie invariant gegenüber Rotation sind, sodass, wenn das umhüllte Element rotiert, die Begrenzungskugel immer noch dieselbe bleibt. Ihr Hauptnachteil ist, dass, es sei denn, das umhüllte Objekt ist tatsächlich kugelförmig, die Umhüllung normalerweise nicht sehr gut passt (zum Beispiel würde das Umhüllen einer Person mit einer Begrenzungskugel viele Fehlalarme verursachen, während eine AABB eine bessere Passform wäre).

Punkt vs. Kugel

Um zu überprüfen, ob eine Kugel einen Punkt enthält, müssen wir den Abstand zwischen dem Punkt und dem Mittelpunkt der Kugel berechnen. Wenn dieser Abstand kleiner oder gleich dem Radius der Kugel ist, befindet sich der Punkt innerhalb der Kugel.

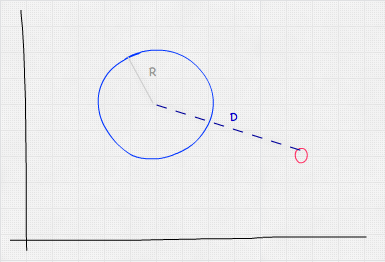
Berücksichtigt man, dass der euklidische Abstand zwischen zwei Punkten A und B $\sqrt{(A_x - B_x)^2 + (A_y - B_y)^2 + (A_z - B_z)^2}$ ist, würde sich unsere Formel zur Kollisionsdetektion von Punkt vs. Kugel folgendermaßen darstellen:

f(P,S) = S_{radius} \ge \sqrt{(P_x - S_x)^2 + (P_y - S_y)^2 + (P_z - S_z)^2}

Oder in JavaScript:

function isPointInsideSphere(point, sphere) {
  // we are using multiplications because is faster than calling Math.pow
  const distance = Math.sqrt(
    (point.x - sphere.x) * (point.x - sphere.x) +
      (point.y - sphere.y) * (point.y - sphere.y) +
      (point.z - sphere.z) * (point.z - sphere.z),
  );
  return distance < sphere.radius;
}

Hinweis: Der obige Code enthält eine Quadratwurzel, deren Berechnung teuer sein kann. Eine einfache Optimierung, um dies zu vermeiden, besteht darin, den quadratischen Abstand mit dem quadratischen Radius zu vergleichen, sodass die optimierte Gleichung stattdessen distanceSqr < sphere.radius * sphere.radius verwenden würde.

Kugel vs. Kugel

Der Test Kugel vs. Kugel ist dem Test Punkt vs. Kugel ähnlich. Was wir hier testen müssen, ist, dass der Abstand zwischen den Mittelpunkten der Kugeln kleiner oder gleich der Summe ihrer Radien ist.

Handgezeichnete Darstellung von zwei sich teilweise überlappenden Kreisen. Jeder Kreis (unterschiedlicher Größen) hat eine leichte Radiuslinie, die von seinem Mittelpunkt zu seinem Rand verläuft, mit R bezeichnet. Die Entfernung wird durch eine gepunktete Linie, die D bezeichnet wird, dargestellt und verbindet die Mittelpunkte beider Kreise.

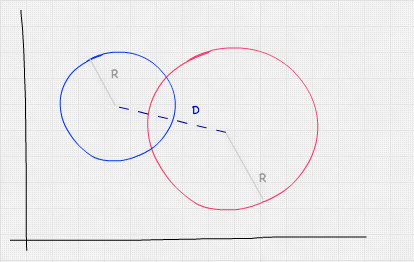
Mathematisch sieht das so aus:

f(A,B) = \sqrt{(A_x - B_x)^2 + (A_y - B_y)^2 + (A_z - B_z)^2} \le A_{radius} + B_{radius}

Oder in JavaScript:

function intersect(sphere, other) {
  // we are using multiplications because it's faster than calling Math.pow
  const distance = Math.sqrt(
    (sphere.x - other.x) * (sphere.x - other.x) +
      (sphere.y - other.y) * (sphere.y - other.y) +
      (sphere.z - other.z) * (sphere.z - other.z),
  );
  return distance < sphere.radius + other.radius;
}

Kugel vs. AABB

Zu testen, ob eine Kugel und eine AABB kollidieren, ist etwas komplizierter, aber immer noch einfach und schnell. Ein logischer Ansatz wäre, jeden Scheitelpunkt der AABB zu überprüfen, indem man für jeden einen Punkt-gegen-Kugel-Test durchführt. Dies ist jedoch übertrieben — das Testen aller Scheitelpunkte ist unnötig, da wir uns damit begnügen können, die Entfernung zwischen dem nächsten Punkt der AABB (nicht unbedingt ein Scheitelpunkt) und dem Mittelpunkt der Kugel zu berechnen und zu prüfen, ob sie kleiner oder gleich dem Radius der Kugel ist. Wir können diesen Wert erhalten, indem wir den Mittelpunkt der Kugel an die Grenzen der AABB klemmen.

Handgezeichnete Darstellung eines Quadrats, das teilweise den oberen Teil eines Kreises überlappt. Der Radius wird durch eine leichte Linie, die mit R bezeichnet ist, dargestellt. Die Entfernungsline geht von der Mitte des Kreises bis zum nächsten Punkt des Quadrats.

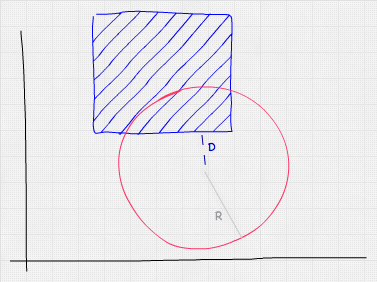
In JavaScript würden wir diesen Test folgendermaßen durchführen:

function intersect(sphere, box) {
  // get box closest point to sphere center by clamping
  const x = Math.max(box.minX, Math.min(sphere.x, box.maxX));
  const y = Math.max(box.minY, Math.min(sphere.y, box.maxY));
  const z = Math.max(box.minZ, Math.min(sphere.z, box.maxZ));

  // this is the same as isPointInsideSphere
  const distance = Math.sqrt(
    (x - sphere.x) * (x - sphere.x) +
      (y - sphere.y) * (y - sphere.y) +
      (z - sphere.z) * (z - sphere.z),
  );

  return distance < sphere.radius;
}

Verwendung einer Physik-Engine

3D-Physik-Engines bieten Algorithmen zur Kollisionsdetektion, die meist ebenfalls auf Begrenzungsvolumen basieren. Eine Physik-Engine funktioniert, indem sie einen physischen Körper erstellt, der normalerweise an eine visuelle Darstellung angeheftet ist. Dieser Körper hat Eigenschaften wie Geschwindigkeit, Position, Rotation, Drehmoment usw. und auch eine physische Form. Diese Form wird in den Kollisionsdetektions-Berechnungen berücksichtigt.

Wir haben eine Live-Demo zur Kollisionsdetektion (mit Quellcode) vorbereitet, die Sie betrachten können, um solche Techniken in Aktion zu sehen — diese verwendet die Open-Source-3D-Physik-Engine cannon.js.

Siehe auch

Verwandte Artikel bei MDN:

Externe Ressourcen:

Einfache Schnittstellentests für Spiele auf Game Developer
Begrenzungsvolumen auf Wikipedia

Help improve MDN

Learn how to contribute Diese Seite wurde automatisch aus dem Englischen übersetzt.

Übersetzung auf GitHub anzeigen • Fehler mit dieser Übersetzung melden